pacman::p_load(sf, terra, spatstat,
maptools, tmap, tidyverse)4 1st Order Spatial Point Patterns Analysis Methods
4.1 Overview
Spatial Point Pattern Analysis is the evaluation of the pattern or distribution, of a set of points on a surface. The point can be location of:
- events such as crime, traffic accident and disease onset, or
- business services (coffee and fastfood outlets) or facilities such as childcare and eldercare.
Using appropriate functions of spatstat, this hands-on exercise aims to discover the spatial point processes of childecare centres in Singapore.
The specific questions we would like to answer are as follows:
- are the childcare centres in Singapore randomly distributed throughout the country?
- if the answer is not, then the next logical question is where are the locations with higher concentration of childcare centres?
4.2 The data
To provide answers to the questions above, three data sets will be used. They are:
CHILDCARE, a point feature data providing both location and attribute information of childcare centres. It was downloaded from data.gov.sg and is in geojson format.MPSZ2019, a polygon feature data providing information of URA 2019 Master Plan Planning Subzone boundary data. It is in ESRI shapefile format. This data set was also downloaded from data.gov.sg.
4.3 Installing and Loading the R packages
In this hands-on exercise, five R packages will be used, they are:
- sf, a relatively new R package specially designed to import, manage and process vector-based geospatial data in R.
- spatstat, which has a wide range of useful functions for point pattern analysis. In this hands-on exercise, it will be used to perform 1st- and 2nd-order spatial point patterns analysis and derive kernel density estimation (KDE) layer.
- terra: The terra package is a modern spatial data analysis package designed to replace the raster package. It offers improved speed and efficiency when working with both raster and vector spatial data, particularly with large datasets. terra provides functionalities for creating, reading, manipulating, and writing raster and vector data, and it’s built on top of GDAL and PROJ libraries for enhanced performance. In this hands-on exercise, it will be used to convert image output generate by spatstat into terra format.
- maptools which provides a set of tools for manipulating geographic data. In this hands-on exercise, we mainly use it to convert Spatial objects into ppp format of spatstat.
- tmap which provides functions for plotting cartographic quality static point patterns maps or interactive maps by using leaflet API.
Use the code chunk below to install and launch the five R packages.
4.4 Spatial Data Wrangling
4.4.1 Importing the spatial data
In this section, st_read() of sf package will be used to import these two geospatial data sets into R.
To import the childcare services data, the code chunk below will be used.
childcare_sf <- st_read("chap04/data/ChildCareServices.geojson") %>%
st_transform(crs = 3414)Reading layer `ChildCareServices' from data source
`C:\tskam\r4gdsa\chap04\data\ChildCareServices.geojson' using driver `GeoJSON'
Simple feature collection with 1925 features and 2 fields
Geometry type: POINT
Dimension: XYZ
Bounding box: xmin: 103.6878 ymin: 1.247759 xmax: 103.9897 ymax: 1.462134
z_range: zmin: 0 zmax: 0
Geodetic CRS: WGS 84Note that st_transform() is used in the code chunk above to re-project the geospatial data to SVY21 projected coordinates system.
To import the planning subzone boundary layer, the code chunk below will be used.
mpsz_sf <- st_read(dsn = "chap04/data",
layer="MPSZ2019")Reading layer `MPSZ2019' from data source `C:\tskam\r4gdsa\chap04\data' using driver `ESRI Shapefile'
Simple feature collection with 332 features and 8 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
Projected CRS: SVY21 / Singapore TMAlthough st_read() is used to import both data sets but the arguments used are not the same. This is because the planning subzone data is stored in ESRI shapefile format.
Before we can use these data for analysis, it is important for us to ensure that they are projected in same projection system.
Using the appropriate sf function you learned in Hands-on Exercise 2, retrieve the referencing system information of these geospatial data.
Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Coordinate Reference System:
User input: SVY21 / Singapore TM
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Notice that childcare_sf is not in projected coordinates system.
Using the method you learned in Lesson 2, transform the projection of childcare_sf into SVY21.
4.4.2 Mapping the geospatial data sets
After checking the referencing system of each geospatial data data frame, it is also useful for us to plot a map to show their spatial patterns.
Using the mapping methods you learned in Hands-on Exercise 3, prepare a map as shown below.
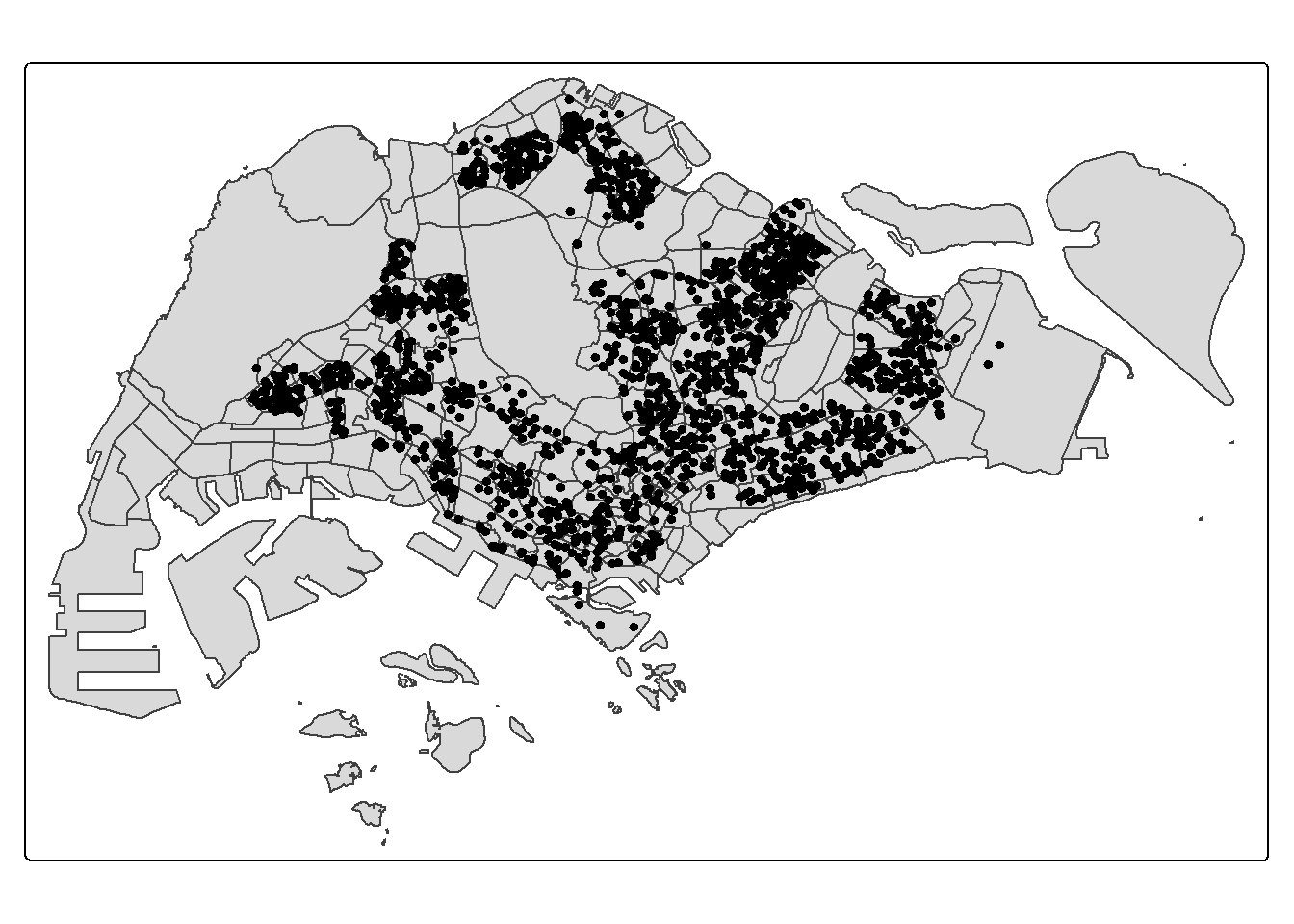
Notice that all the geospatial layers are within the same map extend. This shows that their referencing system and coordinate values are referred to similar spatial context. This is very important in any geospatial analysis.
Alternatively, we can also prepare a interactive point symbol map by using the code chunk below.
tmap_mode('view')
tm_shape(childcare_sf)+
tm_dots()tmap_mode('plot')Notice that at the interactive mode, tmap is using leaflet for R API. The advantage of this interactive pin map is it allows us to navigate and zoom around the map freely. We can also query the information of each simple feature (i.e. the point) by clicking of them. Last but not least, you can also change the background of the internet map layer. Currently, three internet map layers are provided. They are: ESRI.WorldGrayCanvas, OpenStreetMap, and ESRI.WorldTopoMap. The default is ESRI.WorldGrayCanvas.
Always remember to switch back to plot mode after the interactive map. This is because, each interactive mode will consume a connection. You should also avoid displaying ecessive numbers of interactive maps (i.e. not more than 10) in one RMarkdown document when publish on Netlify.
4.5 Geospatial Data wrangling
spatstat relies on its own specific data structures like ppp (planar point pattern) for point data and owin for observation windows. In this section, you will learn how to convert sf (Simple Features) objects into spatstat ppp and owin object.
4.5.1 Converting sf data frames to ppp class
spatstat requires the point event data in ppp object form. The code chunk below uses [as.ppp()] of spatstat package to convert childcare_sf to ppp format.
childcare_ppp <- as.ppp(childcare_sf)Next, class() of Base R will be used to verify the object class of childcare_ppp.
class(childcare_ppp)[1] "ppp"Great, it is in ppp object class!
You can take a quick look at the summary statistics of the newly converted ppp object by using the code chunk below.
summary(childcare_ppp)Marked planar point pattern: 1925 points
Average intensity 2.417323e-06 points per square unit
Coordinates are given to 11 decimal places
Mark variables: Name, Description
Summary:
Name Description
Length:1925 Length:1925
Class :character Class :character
Mode :character Mode :character
Window: rectangle = [11810.03, 45404.24] x [25596.33, 49300.88] units
(33590 x 23700 units)
Window area = 796335000 square units4.5.2 Creating owin object
When analysing spatial point patterns, it is a good practice to confine the analysis with a geographical area like Singapore boundary. In spatstat, an object called owin is specially designed to represent this polygonal region.
The code chunk below, as.owin() of spatstat is used to covert mpsz_sf into owin object of spatstat.
sg_owin <- as.owin(mpsz_sf)Again, class() will be used to verify the object class of sg_owin.
class(sg_owin)[1] "owin"The result above confirmed that sg_owin is indeed in owin object.
sg_owin object can be displayed by using plot() function.
plot(sg_owin)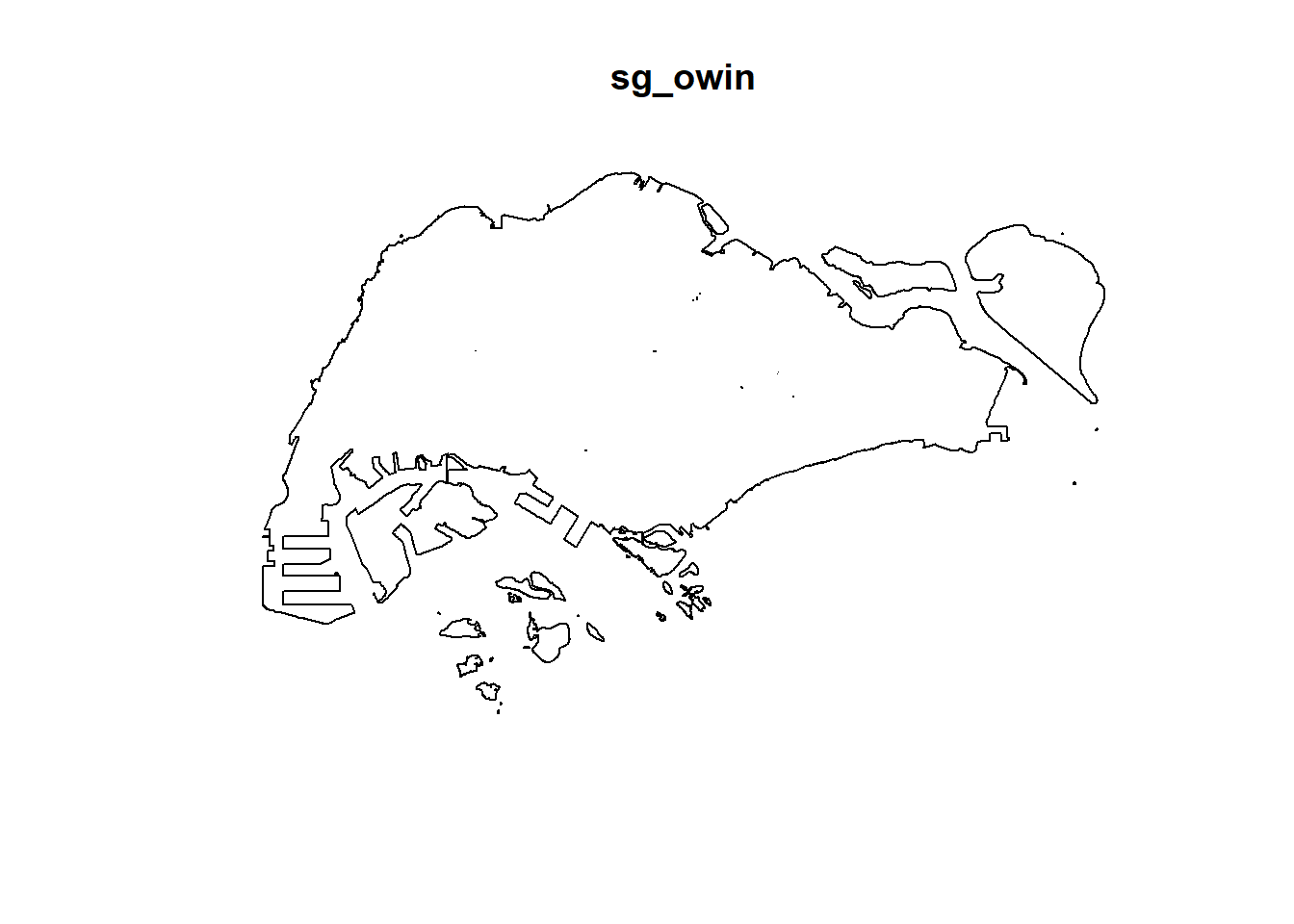
and summary() function of Base R.
summary(sg_owin)Window: polygonal boundary
78 separate polygons (33 holes)
vertices area relative.area
polygon 1 285 1.61128e+06 2.05e-03
polygon 2 719 5.40368e+07 6.89e-02
polygon 3 44 2.26577e+03 2.89e-06
polygon 4 27 1.50315e+04 1.92e-05
polygon 5 709 1.28815e+07 1.64e-02
polygon 6 (hole) 41 -4.01660e+04 -5.12e-05
polygon 7 (hole) 317 -5.11280e+04 -6.51e-05
polygon 8 77 3.29939e+05 4.20e-04
polygon 9 (hole) 3 -4.14100e-04 -5.28e-13
polygon 10 30 2.80002e+04 3.57e-05
polygon 11 (hole) 4 -2.86396e-01 -3.65e-10
polygon 12 (hole) 3 -1.81439e-04 -2.31e-13
polygon 13 (hole) 3 -8.68789e-04 -1.11e-12
polygon 14 (hole) 3 -5.99531e-04 -7.64e-13
polygon 15 (hole) 3 -3.04560e-04 -3.88e-13
polygon 16 (hole) 3 -4.46108e-04 -5.68e-13
polygon 17 (hole) 5 -2.44408e-04 -3.11e-13
polygon 18 (hole) 5 -3.64686e-02 -4.65e-11
polygon 19 71 8.18750e+03 1.04e-05
polygon 20 (hole) 38 -7.79904e+03 -9.94e-06
polygon 21 91 1.49663e+04 1.91e-05
polygon 22 (hole) 3 -3.79135e-02 -4.83e-11
polygon 23 (hole) 395 -7.38124e+03 -9.41e-06
polygon 24 40 1.38607e+04 1.77e-05
polygon 25 (hole) 11 -8.36705e+01 -1.07e-07
polygon 26 (hole) 3 -2.33435e-03 -2.97e-12
polygon 27 45 2.51218e+03 3.20e-06
polygon 28 139 3.22293e+03 4.11e-06
polygon 29 148 3.10395e+03 3.96e-06
polygon 30 (hole) 4 -1.72650e-04 -2.20e-13
polygon 31 75 1.73526e+04 2.21e-05
polygon 32 83 5.28920e+03 6.74e-06
polygon 33 211 4.70521e+05 6.00e-04
polygon 34 106 3.04104e+03 3.88e-06
polygon 35 264 1.50631e+06 1.92e-03
polygon 36 71 5.63061e+03 7.17e-06
polygon 37 10 1.99717e+02 2.54e-07
polygon 38 (hole) 3 -1.37223e-02 -1.75e-11
polygon 39 487 2.06117e+06 2.63e-03
polygon 40 155 2.67502e+05 3.41e-04
polygon 41 1020 1.27781e+06 1.63e-03
polygon 42 (hole) 12 -5.81913e-01 -7.41e-10
polygon 43 (hole) 4 -6.55702e-01 -8.36e-10
polygon 44 (hole) 7 -6.28298e-05 -8.01e-14
polygon 45 65 8.42861e+04 1.07e-04
polygon 46 (hole) 3 -1.20875e-01 -1.54e-10
polygon 47 47 3.82087e+04 4.87e-05
polygon 48 6 4.50259e+02 5.74e-07
polygon 49 129 9.53761e+04 1.22e-04
polygon 50 (hole) 3 -3.23305e-04 -4.12e-13
polygon 51 4 2.69313e+02 3.43e-07
polygon 52 1045 4.44510e+06 5.66e-03
polygon 53 22 6.74651e+03 8.60e-06
polygon 54 59 3.43150e+04 4.37e-05
polygon 55 14 5.86546e+03 7.47e-06
polygon 56 94 5.96187e+04 7.60e-05
polygon 57 234 2.08755e+06 2.66e-03
polygon 58 10 4.90942e+02 6.26e-07
polygon 59 232 4.72886e+05 6.03e-04
polygon 60 (hole) 13 -3.91907e+02 -4.99e-07
polygon 61 15 4.03300e+04 5.14e-05
polygon 62 227 1.10308e+06 1.41e-03
polygon 63 10 6.60195e+03 8.41e-06
polygon 64 19 3.09221e+04 3.94e-05
polygon 65 145 9.61782e+05 1.23e-03
polygon 66 30 4.28933e+03 5.47e-06
polygon 67 37 1.29481e+04 1.65e-05
polygon 68 4 9.47108e+01 1.21e-07
polygon 69 (hole) 3 -3.39815e-04 -4.33e-13
polygon 70 (hole) 3 -4.52041e-05 -5.76e-14
polygon 71 (hole) 3 -3.90173e-05 -4.97e-14
polygon 72 (hole) 3 -9.59845e-05 -1.22e-13
polygon 73 (hole) 8 -4.28707e-01 -5.46e-10
polygon 74 (hole) 4 -2.18619e-04 -2.79e-13
polygon 75 (hole) 6 -8.37554e-01 -1.07e-09
polygon 76 (hole) 5 -2.92235e-04 -3.72e-13
polygon 77 15316 7.00834e+08 8.93e-01
polygon 78 (hole) 3 -7.43616e-06 -9.48e-15
enclosing rectangle: [2667.54, 56396.44] x [15748.72, 50256.33] units
(53730 x 34510 units)
Window area = 784784000 square units
Fraction of frame area: 0.4234.5.3 Combining point events object and owin object
In this last step of geospatial data wrangling, we will extract childcare events that are located within Singapore by using the code chunk below.
childcareSG_ppp = childcare_ppp[sg_owin]The output object combined both the point and polygon feature in one ppp object class as shown below.
summary(childcareSG_ppp)DIY: Using the method you learned in previous exercise, plot the newly derived childcareSG_ppp as shown below.
4.6 First-order Spatial Point Patterns Analysis
In this section, you will learn how to perform first-order SPPA by using spatstat package. The hands-on exercise will focus on:
- deriving kernel density estimation (KDE) layer for visualising and exploring the intensity of point processes,
- performing Confirmatory Spatial Point Patterns Analysis by using Nearest Neighbour statistics.
4.6.1 Kernel Density Estimation
In this section, you will learn how to compute the kernel density estimation (KDE) of childcare services in Singapore.
4.6.1.1 Computing kernel density estimation using automatic bandwidth selection method
The code chunk below computes a kernel density by using the following configurations of density() of spatstat:
- bw.diggle() automatic bandwidth selection method. Other recommended methods are bw.CvL(), bw.scott() or bw.ppl().
- The smoothing kernel used is gaussian, which is the default. Other smoothing methods are: “epanechnikov”, “quartic” or “disc”.
- The intensity estimate is corrected for edge effect bias by using method described by Jones (1993) and Diggle (2010, equation 18.9). The default is FALSE.
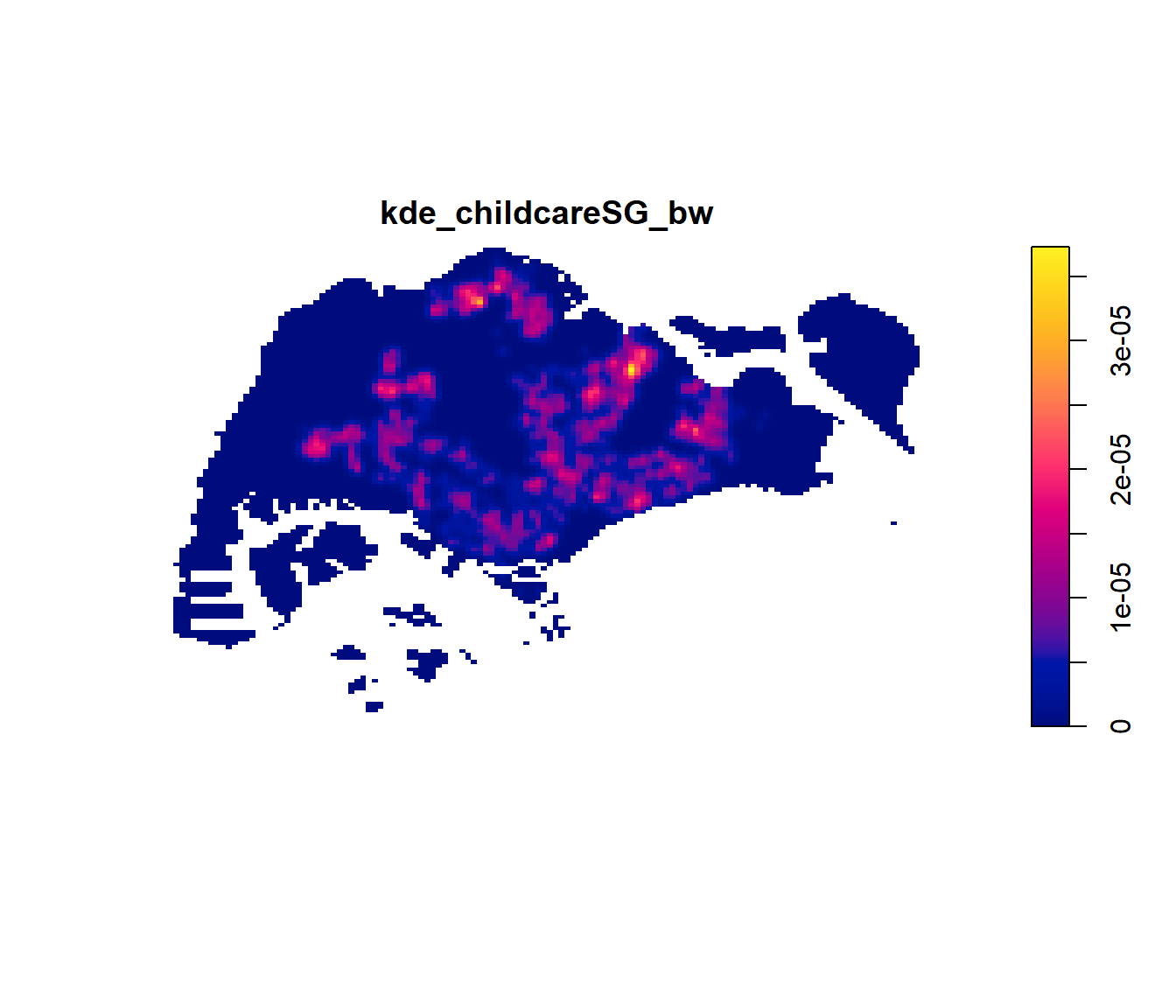
kde_childcareSG_bw <- density(childcareSG_ppp,
sigma=bw.diggle,
edge=TRUE,
kernel="gaussian") The output of density() of spatstat is an im class, represents a two-dimensional pixel image. It’s a class used to store and manipulate raster data, where the spatial domain is divided into a grid of rectangular pixels. Each pixel has an associated value, which can be numerical or a factor.
The plot() function of Base R is then used to display the kernel density derived.
plot(kde_childcareSG_bw)
summary(kde_childcareSG_bw)real-valued pixel image
128 x 128 pixel array (ny, nx)
enclosing rectangle: [2667.538, 56396.44] x [15748.72, 50256.33] units
dimensions of each pixel: 420 x 269.5907 units
Image is defined on a subset of the rectangular grid
Subset area = 784443200.264818 square units
Subset area fraction = 0.423
Pixel values (inside window):
range = [-1.294981e-20, 3.727443e-05]
integral = 1927.013
mean = 2.456536e-06The density values of the output range from 0 to 0.00003727443 which is way too small to comprehend. This is because the default unit of measurement of svy21 is in meter. As a result, the density values computed is in “number of points per square meter”.
Before we move on to next section, it is good to know that you can retrieve the bandwidth used to compute the kde layer by using the code chunk below.
bw <- bw.diggle(childcareSG_ppp)
bw sigma
295.4419 4.6.1.2 Rescalling KDE values
In the code chunk below, rescale.ppp() is used to covert the unit of measurement from meter to kilometer.
childcareSG_ppp.km <- rescale.ppp(childcareSG_ppp, 1000, "km")Now, we can re-run density() using the resale data set and plot the output kde map.
kde_childcareSG.bw <- density(childcareSG_ppp.km,
sigma=bw.diggle,
edge=TRUE,
kernel="gaussian")Next, plot() is used to plot the kde object as shown below.
plot(kde_childcareSG.bw)
Notice that output image looks identical to the earlier version, the only changes in the data values (refer to the legend).
4.6.2 Working with different automatic badwidth methods
Beside bw.diggle(), there are three other spatstat functions can be used to determine the bandwidth, they are: bw.CvL(), bw.scott(), and bw.ppl().
Let us take a look at the bandwidth return by these automatic bandwidth calculation methods by using the code chunk below.
bw.CvL(childcareSG_ppp.km) sigma
4.543204 bw.scott(childcareSG_ppp.km) sigma.x sigma.y
2.159749 1.396455 bw.ppl(childcareSG_ppp.km) sigma
0.3897071 bw.diggle(childcareSG_ppp.km) sigma
0.2954419 Baddeley et. (2016) suggested the use of the bw.ppl() algorithm because past experience shown that it tends to produce the more appropriate values when the pattern consists predominantly of tight clusters. But they also insist that if the purpose of once study is to detect a single tight cluster in the midst of random noise then the bw.diggle() method seems to work best.
The code chunk beow will be used to compare the output of using bw.diggle and bw.ppl methods.
kde_childcareSG.ppl <- density(childcareSG_ppp.km,
sigma=bw.ppl,
edge=TRUE,
kernel="gaussian")
par(mfrow=c(1,2))
plot(kde_childcareSG.bw, main = "bw.diggle")
plot(kde_childcareSG.ppl, main = "bw.ppl")
4.6.3 Working with different kernel methods
By default, the kernel method used in density.ppp() is gaussian. But there are three other options, namely: Epanechnikov, Quartic and Dics.
The code chunk below will be used to compute three more kernel density estimations by using these three kernel function.
par(mfrow=c(2,2))
plot(density(childcareSG_ppp.km,
sigma=bw.ppl,
edge=TRUE,
kernel="gaussian"),
main="Gaussian")
plot(density(childcareSG_ppp.km,
sigma=bw.ppl,
edge=TRUE,
kernel="epanechnikov"),
main="Epanechnikov")
plot(density(childcareSG_ppp.km,
sigma=bw.ppl,
edge=TRUE,
kernel="quartic"),
main="Quartic")
plot(density(childcareSG_ppp.km,
sigma=bw.ppl,
edge=TRUE,
kernel="disc"),
main="Disc")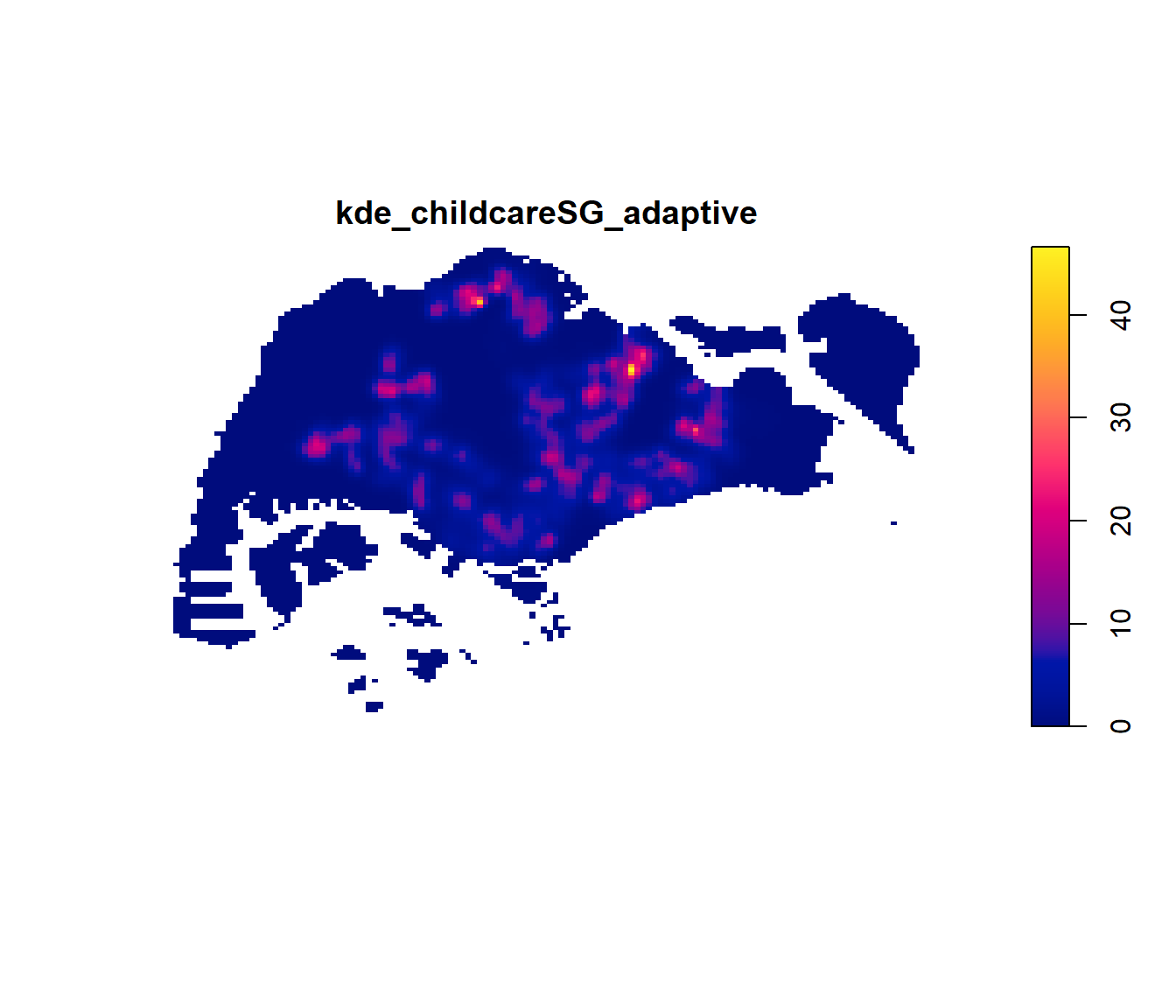
4.7 Fixed and Adaptive KDE
4.7.1 Computing KDE by using fixed bandwidth
Next, you will compute a KDE layer by defining a bandwidth of 600 meter. Notice that in the code chunk below, the sigma value used is 0.6. This is because the unit of measurement of childcareSG_ppp.km object is in kilometer, hence the 600m is 0.6km.
kde_childcareSG_600 <- density(childcareSG_ppp.km, sigma=0.6, edge=TRUE, kernel="gaussian")
plot(kde_childcareSG_600)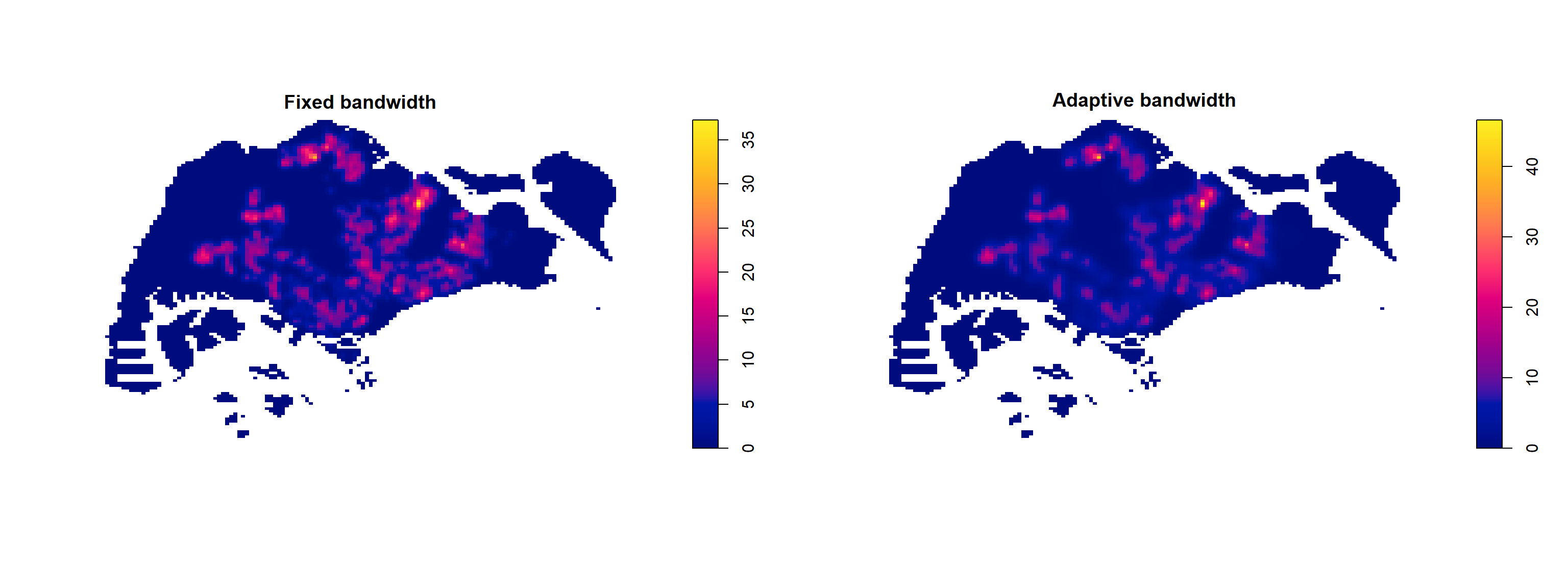
4.7.2 Computing KDE by using adaptive bandwidth
Fixed bandwidth method is very sensitive to highly skew distribution of spatial point patterns over geographical units for example urban versus rural. One way to overcome this problem is by using adaptive bandwidth instead.
In this section, you will learn how to derive adaptive kernel density estimation by using density.adaptive() of spatstat.
kde_childcareSG_adaptive <- adaptive.density(
childcareSG_ppp.km,
method="kernel")
plot(kde_childcareSG_adaptive)
We can compare the fixed and adaptive kernel density estimation outputs by using the code chunk below.
par(mfrow=c(1,2))
plot(kde_childcareSG.bw, main = "Fixed bandwidth")
plot(kde_childcareSG_adaptive, main = "Adaptive bandwidth")
4.7.2.1 Converting gridded output into raster
Next, we will convert the im kernal density objects into SpatRaster object by using rast() of terra package.
kde_childcareSG_bw_terra <- rast(kde_childcareSG.bw)Again, class() is used to verify if kde_childcareSG_bw_terra data are belong to SpatRaster class.
class(kde_childcareSG_bw_terra)[1] "SpatRaster"
attr(,"package")
[1] "terra"Yes, it is indeed in SpatRaster class.
Let us take a look at the properties of kde_childcareSG_bw_terra .
kde_childcareSG_bw_terraclass : SpatRaster
size : 128, 128, 1 (nrow, ncol, nlyr)
resolution : 0.419757, 0.2695907 (x, y)
extent : 2.667538, 56.39644, 15.74872, 50.25633 (xmin, xmax, ymin, ymax)
coord. ref. :
source(s) : memory
name : lyr.1
min value : -1.441026e-14
max value : 3.727443e+01
unit : km Notice that the crs property is empty.
4.7.2.2 Assigning projection systems
In code chunk below, crs() of terra is used to assign the CRS information on kde_childcareSG_bw_terra layer.
crs(kde_childcareSG_bw_terra) <- "EPSG:3414"Let us take a look at the properties of kde_childcareSG_bw_raster RasterLayer.
kde_childcareSG_bw_terraclass : SpatRaster
size : 128, 128, 1 (nrow, ncol, nlyr)
resolution : 0.419757, 0.2695907 (x, y)
extent : 2.667538, 56.39644, 15.74872, 50.25633 (xmin, xmax, ymin, ymax)
coord. ref. : SVY21 / Singapore TM (EPSG:3414)
source(s) : memory
name : lyr.1
min value : -1.441026e-14
max value : 3.727443e+01
unit : km Notice that the coordicates reference (i.e. coord. ref.) is in SVY21 now.
4.7.3 Visualising the output in tmap
Finally, we will display the raster in cartographic quality map using tmap package.
tm_shape(kde_childcareSG_bw_terra) +
tm_raster(col.scale =
tm_scale_continuous(
values = "viridis"),
col.legend = tm_legend(
title = "Density values",
title.size = 0.7,
text.size = 0.7,
bg.color = "white",
bg.alpha = 0.7,
position = tm_pos_in(
"right", "bottom"),
frame = TRUE)) +
tm_graticules(labels.size = 0.7) +
tm_compass() +
tm_layout(scale = 1.0)
Notice that the raster values are encoded explicitly onto the raster pixel using the values in “layer.1” field.
4.7.4 Comparing Spatial Point Patterns using KDE
In this section, you will learn how to compare KDE of childcare at Ponggol, Tampines, Chua Chu Kang and Jurong West planning areas.
4.7.4.1 Extracting study area
The code chunk below will be used to extract the target planning areas.
pg <- mpsz_sf %>%
filter(PLN_AREA_N == "PUNGGOL")
tm <- mpsz_sf %>%
filter(PLN_AREA_N == "TAMPINES")
ck <- mpsz_sf %>%
filter(PLN_AREA_N == "CHOA CHU KANG")
jw <- mpsz_sf %>%
filter(PLN_AREA_N == "JURONG WEST")Plotting target planning areas
par(mfrow=c(2,2))
plot(pg, main = "Ponggol")
plot(tm, main = "Tampines")
plot(ck, main = "Choa Chu Kang")
plot(jw, main = "Jurong West")
4.7.4.2 Creating owin object
Now, we will convert these sf objects into owin objects that is required by spatstat.
pg_owin = as.owin(pg)
tm_owin = as.owin(tm)
ck_owin = as.owin(ck)
jw_owin = as.owin(jw)4.7.4.3 Combining childcare points and the study area
By using the code chunk below, we are able to extract childcare that is within the specific region to do our analysis later on.
childcare_pg_ppp = childcare_ppp[pg_owin]
childcare_tm_ppp = childcare_ppp[tm_owin]
childcare_ck_ppp = childcare_ppp[ck_owin]
childcare_jw_ppp = childcare_ppp[jw_owin]Next, rescale.ppp() function is used to trasnform the unit of measurement from metre to kilometre.
childcare_pg_ppp.km = rescale.ppp(childcare_pg_ppp, 1000, "km")
childcare_tm_ppp.km = rescale.ppp(childcare_tm_ppp, 1000, "km")
childcare_ck_ppp.km = rescale.ppp(childcare_ck_ppp, 1000, "km")
childcare_jw_ppp.km = rescale.ppp(childcare_jw_ppp, 1000, "km")The code chunk below is used to plot these four study areas and the locations of the childcare centres.
par(mfrow=c(2,2))
plot(childcare_pg_ppp.km, main="Punggol")
plot(childcare_tm_ppp.km, main="Tampines")
plot(childcare_ck_ppp.km, main="Choa Chu Kang")
plot(childcare_jw_ppp.km, main="Jurong West")
4.7.4.4 Computing KDE
The code chunk below will be used to compute the KDE of these four planning area. bw.diggle method is used to derive the bandwidth of each
par(mfrow=c(2,2))
plot(density(childcare_pg_ppp.km,
sigma=bw.diggle,
edge=TRUE,
kernel="gaussian"),
main="Punggol")
plot(density(childcare_tm_ppp.km,
sigma=bw.diggle,
edge=TRUE,
kernel="gaussian"),
main="Tempines")
plot(density(childcare_ck_ppp.km,
sigma=bw.diggle,
edge=TRUE,
kernel="gaussian"),
main="Choa Chu Kang")
plot(density(childcare_jw_ppp.km,
sigma=bw.diggle,
edge=TRUE,
kernel="gaussian"),
main="JUrong West")
4.7.4.5 Computing fixed bandwidth KDE
For comparison purposes, we will use 250m as the bandwidth.
par(mfrow=c(2,2))
plot(density(childcare_ck_ppp.km,
sigma=0.25,
edge=TRUE,
kernel="gaussian"),
main="Chou Chu Kang")
plot(density(childcare_jw_ppp.km,
sigma=0.25,
edge=TRUE,
kernel="gaussian"),
main="JUrong West")
plot(density(childcare_pg_ppp.km,
sigma=0.25,
edge=TRUE,
kernel="gaussian"),
main="Punggol")
plot(density(childcare_tm_ppp.km,
sigma=0.25,
edge=TRUE,
kernel="gaussian"),
main="Tampines")
4.8 Nearest Neighbour Analysis
In this section, we will perform the Clark-Evans test of aggregation for a spatial point pattern by using clarkevans.test() of statspat.
The test hypotheses are:
Ho = The distribution of childcare services are randomly distributed.
H1= The distribution of childcare services are not randomly distributed.
The 95% confident interval will be used.
4.8.1 Testing spatial point patterns using Clark and Evans Test
clarkevans.test(childcareSG_ppp,
correction="none",
clipregion="sg_owin",
alternative=c("clustered"),
nsim=99)
Clark-Evans test
No edge correction
Z-test
data: childcareSG_ppp
R = 0.49444, p-value < 2.2e-16
alternative hypothesis: clustered (R < 1)What conclusion can you draw from the test result?
4.8.2 Clark and Evans Test: Choa Chu Kang planning area
In the code chunk below, clarkevans.test() of spatstat is used to performs Clark-Evans test of aggregation for childcare centre in Choa Chu Kang planning area.
clarkevans.test(childcare_ck_ppp,
correction="none",
clipregion=NULL,
alternative=c("two.sided"),
nsim=999)
Clark-Evans test
No edge correction
Z-test
data: childcare_ck_ppp
R = 0.84097, p-value = 0.008866
alternative hypothesis: two-sided4.8.3 Clark and Evans Test: Tampines planning area
In the code chunk below, the similar test is used to analyse the spatial point patterns of childcare centre in Tampines planning area.
clarkevans.test(childcare_tm_ppp,
correction="none",
clipregion=NULL,
alternative=c("two.sided"),
nsim=999)
Clark-Evans test
No edge correction
Z-test
data: childcare_tm_ppp
R = 0.66817, p-value = 6.58e-12
alternative hypothesis: two-sided